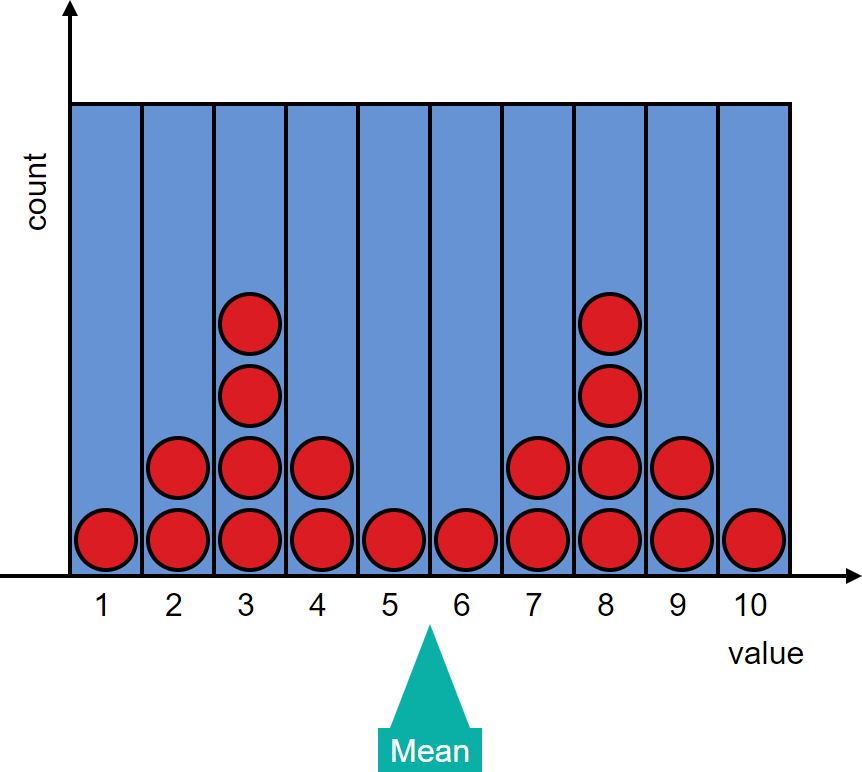
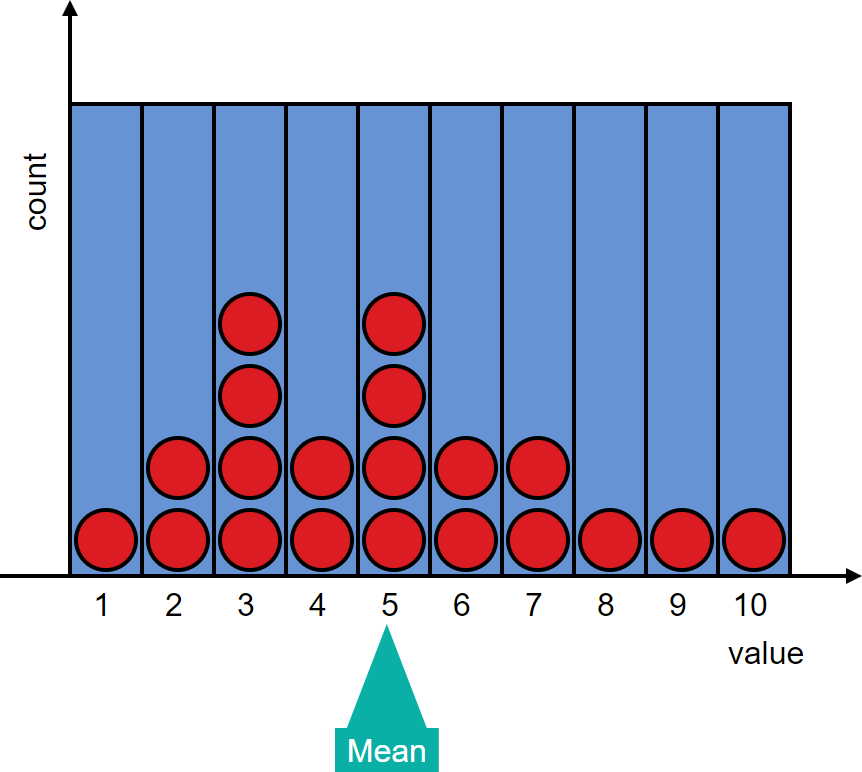
Describing Distribution Shape

Interactive And Practice

(Speaker)

Click the red dots to move them between bins in the distribution. Observe how changes in the distribution of the dots impact the mean, median, and mode. Use the questions and challenges below to guide your exploration.

(Questions)

  1. Question: Create two different distributions each with a mean of 7.
    Answer: There are many possible distributions that have a mean of 7. Two examples are:
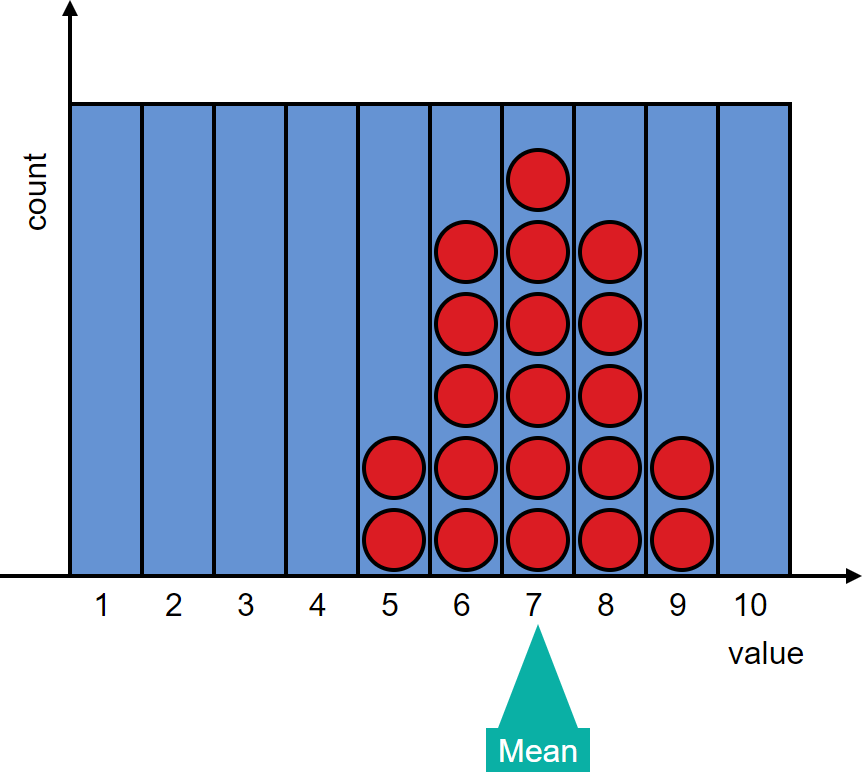
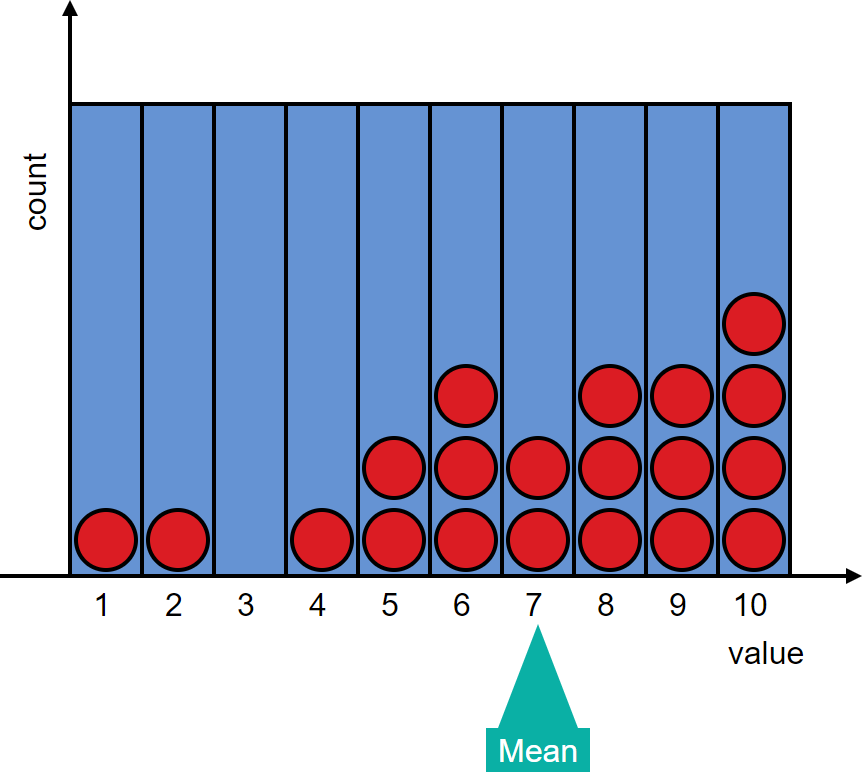
    A distribution has 0 in column 1, 0 in 2, 0 in 3, 0 in 4, 2 in 5, 5 in 6, 6 in 7, 5 in 8, 2 in 9, and 0 in 10. The mean is 7.      A distribution has 1 in column 1, 1 in 2, 0 in 3, 1 in 4, 2 in 5, 3 in 6, 2 in 7, 3 in 8, 3 in 9, and 4 in 10. The mean is 7.
  2. Question: Create a distribution with a mean that corresponds to a bin with no data.
    Answer: Again, there are many possible distributions that fit this criterion. Two examples are:
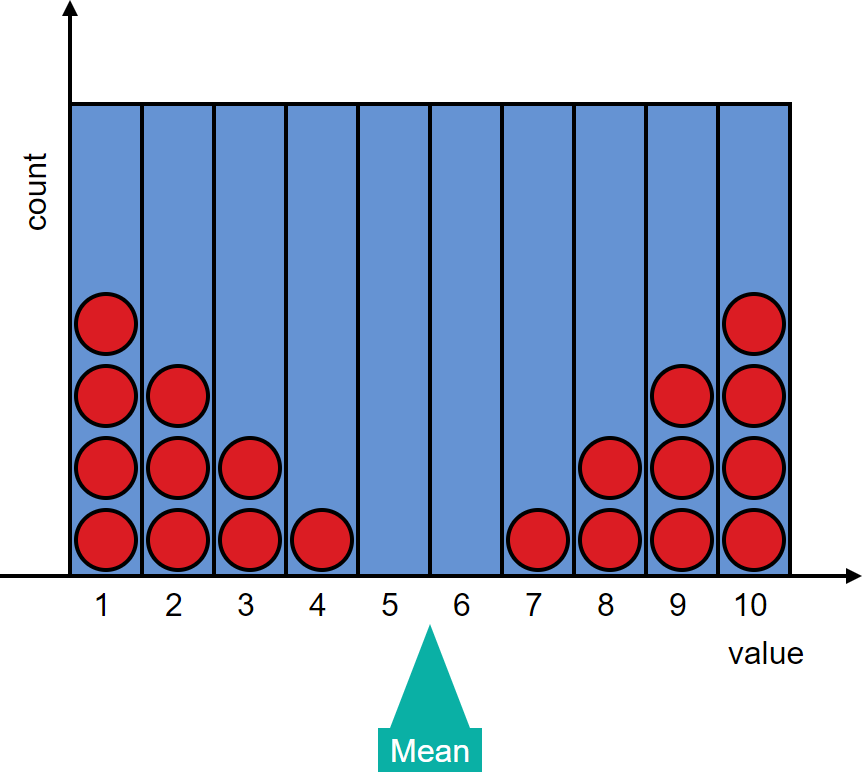
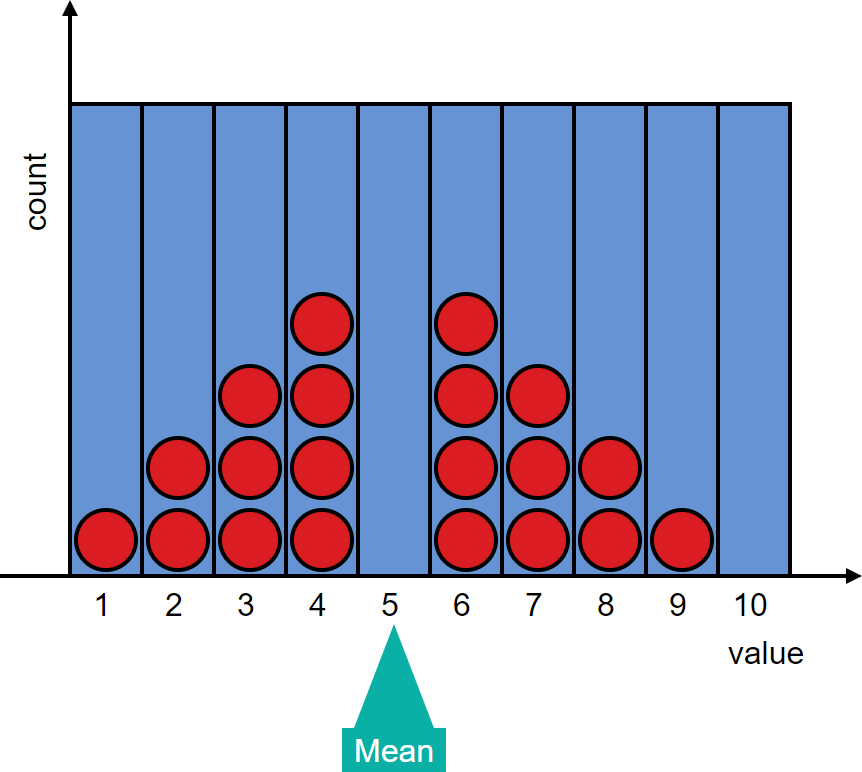
    A distribution has 4 in column 1, 3 in 2, 2 in 3, 1 in 4, 0 in 5, 0 in 6, 1 in 7, 2 in 8, 3 in 9, and 4 in 10. The mean is 5.5.      A distribution has 1 in column 1, 2 in 2, 3 in 3, 4 in 4, 0 in 5, 4 in 6, 3 in 7, 2 in 8, 1 in 9, and 0 in 10. The mean is 5.
  3. Question: Where do you expect the mean to fall in a bimodal distribution?
    Answer: In a symmetric bimodal distribution, the mean would be expected to fall between the two peaks. In an asymmetric bimodal distribution, the mean would depend on the overall shape of the distribution.
    A symmetric distribution has 1 in column 1, 2 in 2, 4 in 3, 2 in 4, 1 in 5, 1 in 6, 2 in 7, 4 in 8, 2 in 9, and 1 in 10. The mean is 5.5.      An asymmetric distribution has 1 in column 1, 2 in 2, 4 in 3, 2 in 4, 4 in 5, 2 in 6, 2 in 7, 1 in 8, 1 in 9, and 1 in 10. The mean is 4.9.